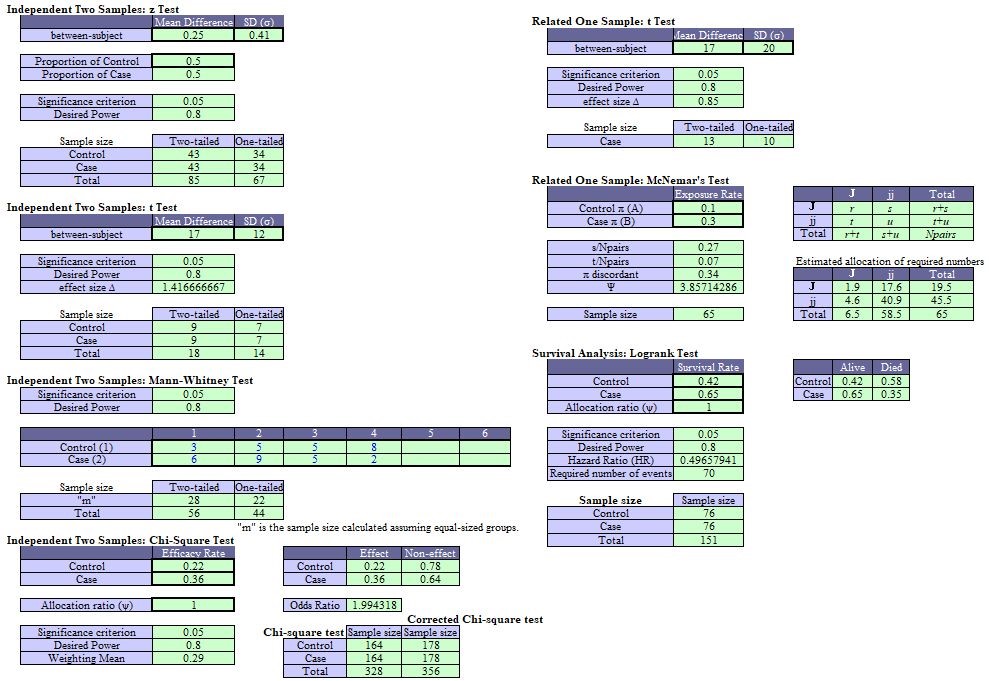
Independent Two Samples: z Test
Exercise:
The mean birth weights of newborn babies in north and south areas of a certain region are 3.53kg and 3.28kg, respectively. The standard deviation of body weight data was 0.41kg.
Estimate required samples numbers for body weight comparison between these two areas with levels of α-error as 0.05 and β-error as 0.1. The sample numbers of north and south areas are assumed equal.
Independent Two Samples: t Test
Exercise:
Two different anti-hypertensive drugs are administered as the pilot study in 2 groups (A and B) of patients with mild hypertension. The peak blood pressures after a certain period were 138mmHg in A group and 121mmHg in B group. The standard deviation σ was assumed as 12mmHg.
Estimate required sample sizes for two-samples t test with levels of α-error as 0.05 and β-error as 0.1.
Independent Two Samples: Mann-Whitney Test
Exercise:
As a pilot study, therapeutic effects of two drugs, a standard drug (1) and newly developed drug (2), on allergic rhinitis were compared. The evaluation of the drug effects was categorized into 4 groups, significantly effective, effective, no change, or exacerbated.
Estimate required samples numbers for Mann-Whitney test with levels of α-error as 0.05 and β-error as 0.1.
Independent Two Samples: Chi-Square Test or Fisher’s Exact Test
Exercise:
As a pilot study, therapeutic effects (effective or not effective) of two treatment protocols (A, B) on a certain disease were compared. The efficacy rate of treatment protocol A was 22%, and that of treatment protocol B was 36%.
Estimate required samples numbers for chi-Square test with levels of α error as 0.05 and β error as 0.1. The allocation ratio of treatment protocols is assumed as 1 : 1.
Related One Sample: t Test
Differences in serum cholesterol levels between pre- and post-dietary therapy and the standard deviation (SD) are shown here.
Estimate required samples numbers for one-sample t test with levels of α error as 0.05 and β error as 0.2.
Related One Sample: McNemar’s Test
Exercise:
The effect of oral rinse after brushing of teeth on dental bacterium was assessed as a pilot study.
The bacterial cultivation before and after the oral rinse treatment was performed. A positive rate of presence of bacteria was 10% before the oral rinse and 30% after the oral rinse.
Estimate required samples numbers for McNemar’s test with levels of α error as 0.05 and β error as 0.1.
Survival Analysis: Logrank Test
Exercise:
In patients with leukemia, the remission rates (survival or death) of treatment of conventional drug and new drug were compared. Survival rates at one year after the new drug introduction was 42% by conventional drug treatment and 65% by new drug treatment, respectively.
Estimate one-year hazard ratio and the number of death cases (event number) with levels of α-error as 0.05 and β-error as 0.1. The allocation ratio of two groups is assumed as 1 : 1.In addition, estimate required sample numbers to compare the survival rates between two groups using a log-rank text.